(Prepare yourself for some really bad math.)
I think this is the very final math problem I ever do, because I find it outrageously boring. But I’ll write it down, just for the sake of whatnot. “Infinity” itself seems, as far as I understand, to be poorly understood; and at the same time I stumbled on an old question I had myself a long time ago and never actually looked into it, that is if functions such as
f(x) = x²
and
h(x) = √x
will reach infinity and if they do, how they do it, because it did not seem all that obvious to me at the time, and neither does it seem obvious to me now.
Now please keep in mind I’m a high school dropout who essentially never touched a math book ever again, so you’re going to be watching some super-simple high school math. Bear with me.
So we have to make a few presumptions.
- We don’t know what infinity is. We just know that it’s out there somewhere, and other than being uncountable, has some other weird properties that we don’t care about at all for this problem.
- We presume that (positive) infinity pops up somewhere somehow when the numbers are becoming larger and larger without end.
- On a 2-dimensional plane there are 2 (positive) infinities, one with y reaching infinity, and one with x reaching infinity.
- We will be using the speed of which a function or series approaches both infinities to draw some conclusions.
- Does it make sense or not?
1. The three main functions we’re using.
For our little thought experiment we will use three simple functions:
- f(x) = x²
- g(x)=x
- h(x) = √x
2. The three main functions drawn out.
Because we’re lazy folk.
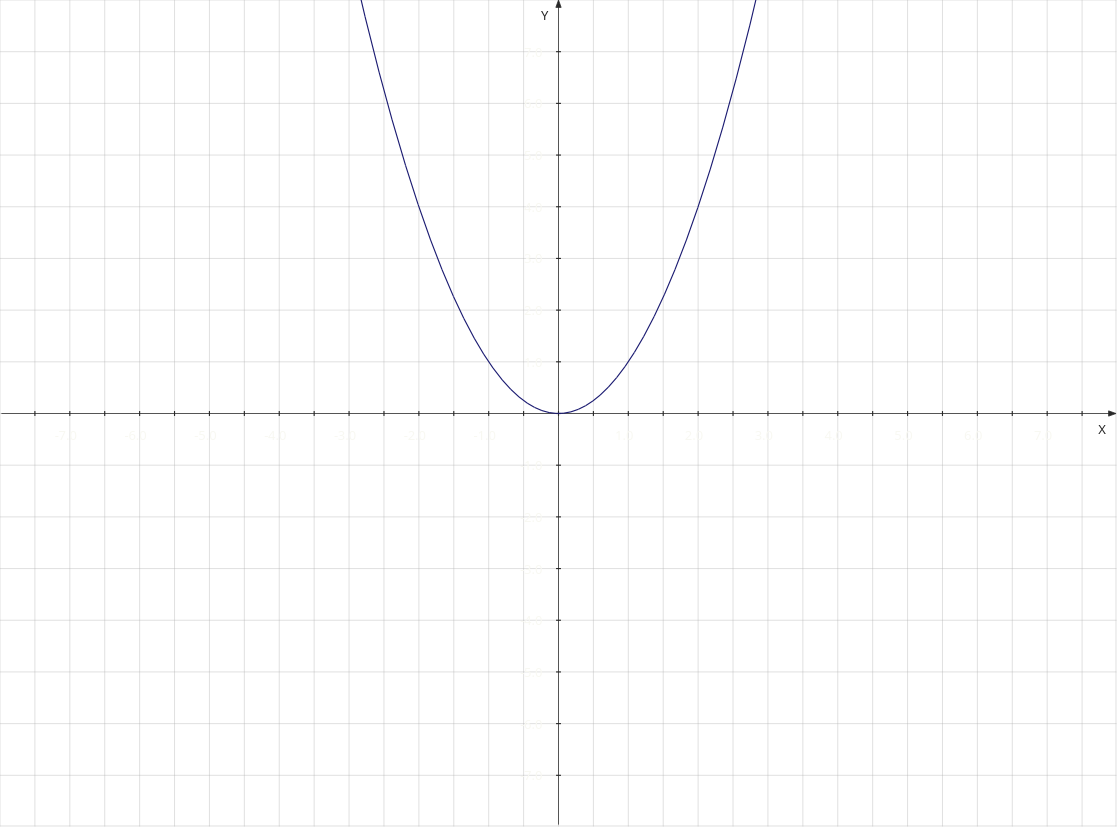
- f(x) = x²
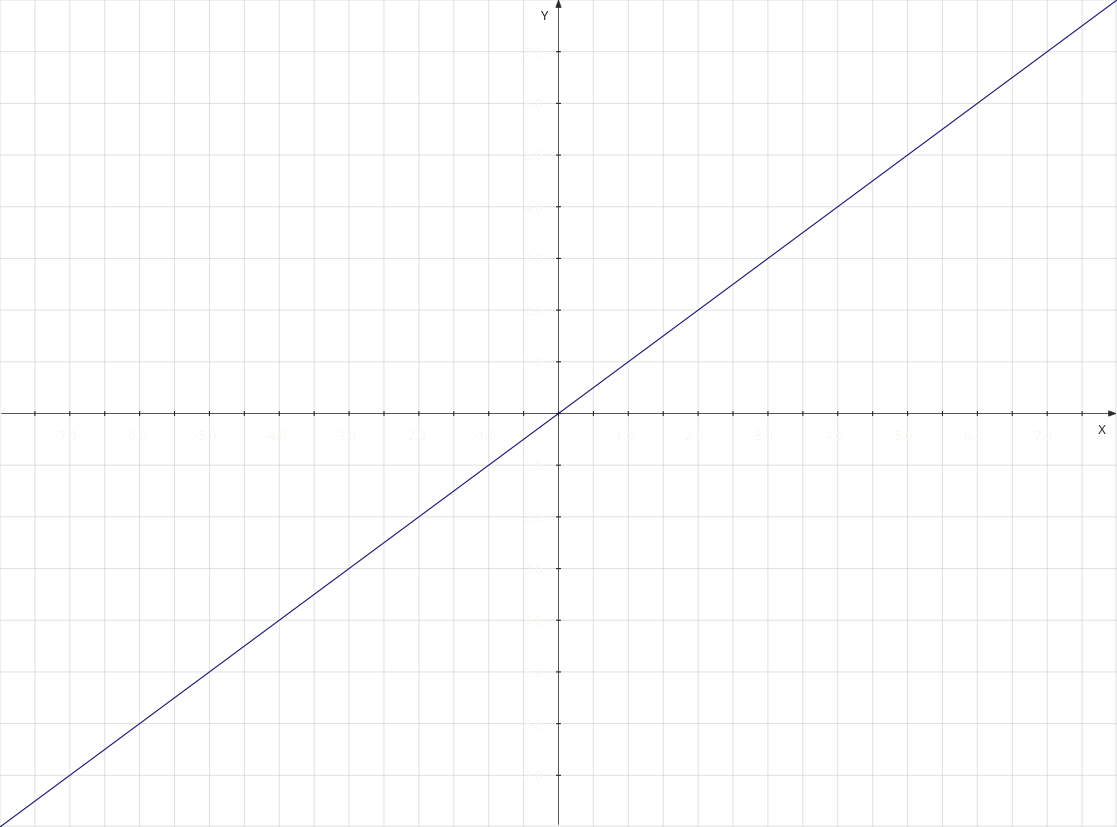
2. g(x)=x
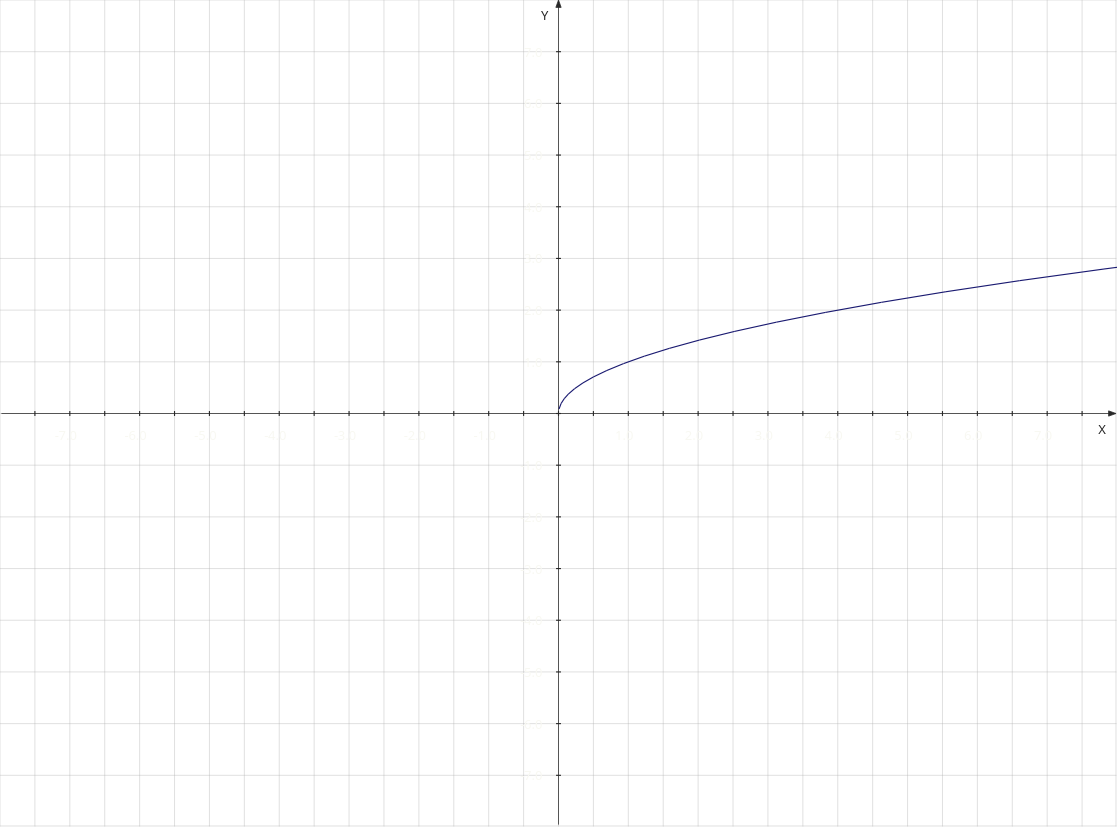
3. h(x) = √x
The graphs are not needed of course, but why not. This is a silly blog post anyway. So the 2nd example g(x)=x is fairly clear: Both positive and negative x and y infinity are going to be reached in equal speed.
The other two graphs are a bit different: Just from watching we can say that f(x) = x² kind of sprints towards the positive and negative y-infinity, and crawls towards the positive and negative x infinity.
To me this and especially h(x) = √x was always pretty clear and raised some questions. With the speed towards y-infinity de-accelerating, how can it ever actually reach infinity? Obviously I understand the logic, which is that just less and less gets added in time but, regardless, infinity will be reached but much slower.
I always smelled something fishy here, which really, don’t take me too seriously here. It might be completely correct what the books and essentially anyone who knows a thing or 2 about math is stating.
But it’s a bit odd. Positive infinity in this case is just some thing out there that you apparently reach when the numbers blow up, which will never happen in the case of h(x) = √x.
However the three functions are all divergent functions, and by definition they will reach infinity isn’t it. So that must be it or so.
4. Let’s do some Kindergarten Math
This will come later.
5. Conclusion
Anyone, how odd is this?
6. Addendum
A strange video popped up in my YouTube recommendation. These days I hardly take them seriously to be very honest, but this was a really good one, and on top of that Yours Truly was capable of understanding it, which is not always the case with math videos. The topic is somewhat related to this blogpost, although on a much higher level obviously, but not ‘impossibly high’ so to say.
So this is superinteresting. I haven’t written chapter 4 out yet; but one of the points would be something very simple: If you continue taking the derivates of the 3 functions you end up with 1 ending in a > 1 (a is just the final result you get after taking the usual derivatives, really, it’s superbasic stuff), in one a=1 and in one the limit of a going to infinity equals zero. So logically speaking the distance of a>1 and a going to infinity is ever-increasing, and just by using some baby-logic we can therefore conclude that when going to infinity the distance will be ever-increasing and therefore, what you would expect is that one of them will never leave the realm of the real numbers.
It might be complete bull of course, but yeah, debunk it, right.
But this video takes another look at it, one that is also somewhat apparent if you look at the three graphs. Essentially of you take the numbers 0 and 1, then going from 1 towards 0 and from 1 towards infinity are mirrored. Which is kinda cool, you know, for aesthetics sake. So essentially if you’re really into it, you can just forget about integers and what not and just treat them like a tool used to software engineers and by evil teachers torturing their poor students over and over again with that nonsense. That probably does not include the transcedentals, but I suspect you can do some trickery with those.
They say in the video that numberlines do not exist for let’s say N-based numbers. I think they are slightly wrong there; you can go two ways: You can abolish the existence of numberlines altogether, or you can have multiples of them, or one that for example in binary has 1 on 1, 10 on 2, 100 on 4, 1000 on 8, etc.
This requires you to know the powers of 2 pretty well of course, but you can also use the decimal one, and base a new one off that; 1,10,11,100,101, 110, 111, 1000, etc. , using the same trickery as you might be doing in decimal, but just binary only. I personally do some trickery every time a 0 is added. Binary blows up really quickly isn’t it.
So they all do have their own numberline; it’s just completely different, which would essentially hint at the fact that we truly construct our numbers, but that’s a different topic.
The funky thing is that you can then train yourself to count in base N only without actually using any of base 10. Which would be so odd in real life, or when talking to someone, but mathematically correct.
So the point is that if you’re good this stuff, which I’m not, then you can actually really get by using the definition that there’s 0, 1 ‘and the rest is a matter of definition’. Maybe apart from pi and e. So you can really write on your test-sheet that ‘sorry, I can’t answer this question, because there are infinitely many ways to write down the supposed answer’. I’m sure that won’t get you an A+, but they, you can.
All right, this post is work in progress (on steroids). But I might keep this problem to have something to do on boring, rainy days where depressing is hitting even harder than usual, cuz yeah, what else do I have to do right.
Will be continued (and rewritten).